Briefly on semopy
semopy stands for Structural Equation Models Optimization in Python and is designed to help statisticians that employ SEM techniques to handle their research in a more Pythonic way. We want to fill a niche of SEM tools in Python that is seemed to be empty as we found ourselves and several other researchers to be unsatisfied using either commercial software or dealing with older computer languages.
semopy package provided completely free of charge and everyone is welcome to make contributions to the project. The developers of semopy promise to keep their eye open for bugs and to consider implementing new features on request.
The package was published in "Structural Equation Modeling: A Multidisciplinary Journal" where we showed that semopy outperforms the popular free package lavaan in terms of both performance, optimization process stability and parameter estimates accuracy. Since then, semopy has faced drastic positive changes and has grown new features, therefore a reader can interpret results presented in the article as an expected minimum. As of today, the actual state of semopy 2+ is best explained in a new article, currently available as a preprint.
Features
- User-friendly syntax
- semopy enjoys lavaan-like syntax for specifying SEM models.
- Arbitrary models
- It's possible to specify a very general SEM model, even the most unorthodox one: all variables can interact with each other be it via covariance relationship or direct regression effects.
- Mean components estimation
- Researcher can estimate intercepts if necessary, either via two-stage procedure or via one-stage procedure through a special model with all exogenous variables ruled out into a mean component.
- Constraints
- Arbitrary constraints (linear and non-linear) can be imposed on the model parameters by a researcher.
- Restricted Maximum Likelihood (REML)
- semopy can facilitate estimating parameters through a REML approach and to obtain unbiased variance estimates simultaneously.
- Random Effects model
- We bred Random Effects model (or Linear Mixed Models/LMM) with SEM to take population structure into account when necessary. With introduction of random effects you can effectively control for clustered data, or even tackle autoregression/dependence across individuals if proper covariance-between-groups matrix is known.
- Gaussian processes model
- The notion of random effects is extended and generelized to an arbitrary dependence structure imposed on a population, making modeling plethora of phenomenas, such as temporal and spatial data.
- Polychoric/Polyserial correlations
- Researcher can hide ordinal variables behind an underlying latent variable and to produce a heterogenous correlation matrix.
- Regularization
- Package user can impose regularization on model parameters.
- Imputation and factor estimation
- semopy can be used to predict data, impute missing values and to estimate factor scores.
- Exploratory Factor Analysis (EFA)
- semopy incorporates some utilities to perform EFA to extract measurement structure from the data.
- Model generation
- Reseachers can generate random models with semopy's model generator to test semopy or other SEM packages features.
- It's fast
- Initially, semopy was designed to be applied to big genomic data, so we had achieving adequate performance in mind.
Example
To give reader a quick example of what kind of SEM models semopy can handle, consider the following model:
# structural part eta3 ~ x1 + x2 eta4 ~ x3 x3 ~ eta1 + eta2 + x1 + x4 x4 ~ eta4 x5 ~ x4 # measurement part eta1 =~ y1 + y2 + y3 eta2 =~ y3 eta3 =~ y4 + y5 eta4 =~ y4 + y6 # additional covariances eta2 ~~ x2 y5 ~~ y6
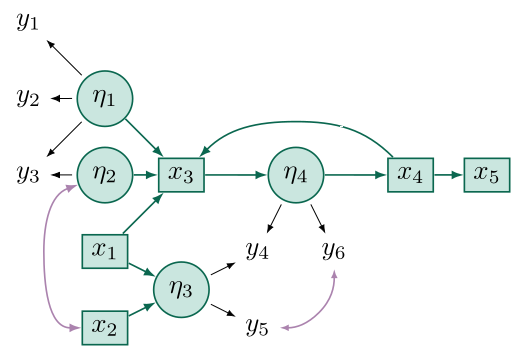
For a quickstart, see the Tutorial section.
Why 2?
Although the package has found a dozen users worldwide previously, its development and usage have been mostly restricted to the internal affairs of developers' laboratory. The package was a mess with certain design decisions that could appear as bugs to an unprepared user. Furthermore, at one point it became increasingly difficult to implement new features as the semopy 1.0+ structure was not designed really well. In July 2020, the package has been rewritten from scratch, and following the Semantic Versioning paradigm semopy versions will henceforth start with a digit "2".
Acknowledgements
semopy development was supported by RFBR Grant No. 18-29-13033. Authors are grateful to the staff of the Mathematical Biology & Bionformatics Laboratory at Peter the Great St. Petersburg Polytechnic University.